Передача теплоты теплопроводностью описывается дифференциальным уравнением теплопроводности, вытекающим из закона сохранения количества тепловой энергии и основного закона теплопроводности (закона Фурье). Приведем вывод этого уравнения для одномерного нестационарного температурного поля.
Рассмотрим изменение теплосодержания элемента стержня длиной dx и площадью поперечного сечения F, равной единице (рис. 4.1).
Изменение теплосодержания ДQ, вызванное изменением АТ температуры Т(х, т) за время Дх в выделенном объеме Д/ = Дх*1:
ах
ДО = CVAT • Дх = Cv —— Дт • Дх. (4.5)
от
Количество теплоты, поступившей за это время через единичную площадь поверхности, может быть определено также через приращение плотности теплового потока Aqx:
ДО = — ДаФ-1 • Дх = Ах ■ Ат.
|
(4.6) |
дх
|
Рис. 4.1. Схема к выводу уравнения теплопроводности для одномерного нестационарного температурного поля |
Из (4.5) и (4.6) с учетом основного закона теплопроводности (4.3) следует:
дТ _ dq
|
дх дх2 |
Cv аГ~
Таким образом, уравнение теплопроводности для одномерного нестационарного температурного поля может быть записано в виде [59]
|
(4.7) |
дТ д2Т дх ® дх2′
Для двухмерного и трехмерного температурных полей уравнение теплопроводности (4.7) примет вид
SHAPE \* MERGEFORMAT ![]()
|
|
|
д2Т д2Т дх2+ ду2 |
|
д2Т д2Т д2Т dx2+dy2+dz2 |
|
,= со |
дх’
Для решения дифференциального уравнения теплопроводности (4.7) задают краевые условия, включающие начальные и граничные условия. Начальное условие задает распределение температуры внутри тела (для одномерного поля — в стержне) в начальный момент времени:
Дх, 0)= /(х),
где f(x) — известная функция. Важным частным случаем является равномерное распределение температуры в начальный момент времени: Т(х,0)=Т0.
Граничные условия задают различными способами. Граничные условия первого рода задают в виде распределения температуры на поверхности тела (на торце стержня) в любой момент времени [59]: Т„(х) = f(x)
Важным частным случаем является задание постоянной температуры: 7„(т) = 7-0.
Граничные условия второго рода задают в виде распределения плотности теплового потока для каждой точки поверхности как функции времени [59]: qn(x)=f(x) и, в частности: Qn(x) = qf0.
Если необходимо охарактеризовать конвективный теплообмен между поверхностью тела и движущейся окружающей средой при постоянном потоке теплоты, используют граничные условия третьего рода: плотность теплового потока q„, уносящегося средой, считают пропорциональной разности температур поверхности тела и среды [59]:
Яп — ot(Tn — 7С),
где а — коэффициент теплообмена, Вт/(м2К).
При этом условия теплообмена на поверхности записывают в виде равенства суммы потоков тепла на поверхности со стороны тела и среды:
|
|
Если вместо окружающей среды в теплообмене участвует еще одно твердое тело, то это граничные условия четвертого рода [59]:
|
|
Перечисленные способы задания краевых условий, хотя и являются наиболее часто применяющимися, не охватывают всех тех случаев, которые могут встретиться в разнообразных технологических задачах. Так, некоторые особенности постановки задач возникают при учете движения твердых тел, соприкасающихся по поверхностям скольжения. Процесс теплообмена еще более усложняется, если трение сопровождается пластическими деформациями одного из тел в некоторой области и тем более, если характеристики сопротивления деформируемой среды являются функциями температуры.
Решением дифференциального уравнения теплопроводности (4.7) является функция Т(х, х), которая при подстановке в уравнение (4.7) обращает его в тождество и, кроме того, удовлетворяет краевым условиям.
|
|
Одним из наиболее простых и важных примеров является решение уравнения теплопроводности для мгновенного плоского источника тепла, вспыхнувшего в начальный момент времени х = 0 в плоскости ZOY, перпендикулярной оси х, т. е. в точке х = % бесконечного стержня с нулевой начальной температурой, и выделившего при этом количество теплоты Q. Поскольку стержень неограниченный, то граничные условия могут быть записаны в виде
(4.8)
Решение уравнения теплопроводности для мгновенного (плоского) источника предложено Томсоном-Кельвином и имеет вид [59]
и-if
|
(4.9) |
|
4ют |
б(хЛ, т)=-г=—exp —
V471C0T
Непосредственной проверкой легко убедиться, что функция (4.9) удовлетворяет уравнению теплопроводности (4.7) и граничным условиям (4.8). Из (4.9) также следует, что функция G(x,^,x) имеет максимум в точке х = % и что количе-
ство теплоты Q в любой момент времени остается неизменным и равным CVB, а также что величина В представляет собой площадь, ограниченную функцией Г(х, т) и осью х.
Функцию 6(х, £, т) называют фундаментальным решением уравнения теплопроводности. Это связано с тем, что с помощью этого решения можно сконструировать решения уравнения теплопроводности для других краевых условий: для этого любой процесс распространения теплоты в твердом теле теплопроводностью представляется как совокупность процессов выравнивания температуры от множества элементарных источников теплоты, распределенных как в пространстве, так и во времени. Результат получается суммированием (интегрированием). Описанный метод решения уравнения теплопроводности называется методом точечных источников теплоты. В качестве примера применения метода источников теплоты рассмотрим задачи о выравнивании температуры, заданной начальным распределением, и об одномерном нестационарном температурном поле полуограниченного стержня, торец которого находится при постоянной температуре.


 2 августа, 2014
2 августа, 2014  Menedjer
Menedjer 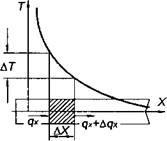
 Опубликовано в рубрике
Опубликовано в рубрике