Воспользуемся идеей метода точечных источников тепла для описания процесса выравнивания температуры в неограниченном стержне. Представим начальные условия, заданные в виде известной функции Т(х,0)= f(x), как суммы бесконечного множества кривых вида [59]:
|
(*-02 4 сот |
|
(*-*02 4сот |
|
dЈ. (4.10) |
|
f(Ј,)dЈ, lim. exp т-»0 у/ 4ясот |
|
Л +°° , Т. е. e(x,0) = |im-7= |V(4)exp T-»0 V47IC0T |
Чтобы доказать справедливость такого представления начального условия, необходимо установить, что записанное в виде интеграла выражение (4.10) при т-> 0 стремится к f(x). Для этого заменим переменную интегрирования £, новой переменной и: £ = х + 2л/ют • и.
После этого выражение (4.10) преобразуется к виду
lim ~7=г ( f[x + 24vn и)ехр(-и2 )du =
Т-*0 4п -00
= f{x)—.L J exp[~u2)du = f(x).
V Я —со
Из этого следует, что функция 0(х, т) удовлетворяет начальному условию. Кроме того, поскольку при х—>±оо подынтегральная функция стремится к нулю, выполняются и граничные условия (4.8). Таким образом, функция [59]
|
(х-4)2 4юх |
|
Г(х, х) = |
|
(4.11) |
|
j>fe)exp |
|
л/4ясот j |
представляет собой решение задачи выравнивания температуры, заданной начальным распределением f(x), в бесконечном стержне.
|
Рис. 4.2. Схема начального и последующего распределений температуры для полуограни — ченного стержня и граничных условий первого рода |
Рассмотрим задачу распределения температуры в полуограниченном стержне, на торце которого поддерживается постоянная температура Тс: Т(0,т)=Тс = const, а начальное рас
пределение температуры Т(х,0) задано функцией f(x) (рис. 4.2), т. е. заданы краевые условия первого рода.
Если вместо переменной Т(х, х) использовать новую переменную Т = Г(х, т)-Гс, то граничные условия запишутся:
Т = Г(х, т)-Тс = 0.
Эти граничные условия будут выполнены, если полубесконечный стержень (0< X < +оо) условно заменим бесконечным (-00 < X < +00), причем начальную температуру в области (х<0) продолжим как нечетную функцию (см. рис. 4.2):
f(x) = — f(-x).
При этом вследствие симметрии распределение температуры будет оставаться нечетным и в последующие моменты времени (т>0), что обеспечит выполнение граничного условия Т = Т(х, х)-Тс = 0.
Применяя формулу (4.11) и разбив бесконечный интервал на два полуогра — ниченных, получим
|
и Jffe)exp |
|
1 |
|
eft; U |
|
Г(х, х)-Гс = |
|
л/4 |
|
4оот |
|
71С0Т |
|
(x-lf 4cox |
|
j ffe)exp |
|
л/4 |
|
71С0Т |
Пользуясь свойством нечетности, в первом слагаемом заменим переменную % на a fiK) на — Ш
|
™-т°- |
к — (4.12)
Если начальная температура постоянна по всей длине стержня
f(x) = Т(х, 0) = Т0= const,
то решение для температуры стержня с постоянной температурой Тс на торце примет вид [59]
X
~
Т(х, х)-Тс 22^ ( 2І
|
(4.13) |
|
к 2 Van |
——-—— = — | ехр^-и* ри = erf То ~ТС Jti о
где erfl —£= — функция ошибок Гаусса.
Зная распределение температуры в любой момент времени, можно определить потери тепла на конце стержня при остывании или расход тепла при нагреве. На основании закона Фурье (4.4) найдем плотность теплового потока
|
Q ф — — X |
|
дх |
дТ<*»» (4.14)
у х=0
Из формулы (4.14) следует, что в начальный период времени (при т 0) плотность теплового потока очень велика, но с течением времени уменьшается. Комплекс теплофизических характеристик є = JxCv называют коэффициентом аккумуляции теплоты или коэффициентом тепловой активности тела.
Определим количество тепла Q, отведенного через торец стержня площадью F при остывании (или подведенного к торцу стержня при нагреве):
Q = FjQoCft = FzTc —LrJ-^L = ^j=TcF yfx. (4.15)
0 л/яол/т л/я
Таким образом, количество тепла, необходимое для поддержания постоян
ной температуры, увеличивается пропорционально корню квадратному из времени нагрева, т. е. сначала быстро, а затем все медленнее.
Определение температурного поля при граничных условиях второго рода (т. е. при задании теплового потока на торце стержня) представляет интерес в связи со многими технологическими задачами. Математическая формулировка этой задачи может быть дана в следующем виде [59]: найти решение уравнения (4.7), удовлетворяющее краевым условиям:
Г(х,0) = Т0= const, X + qc=0,
дх
Г(оо. х)=Го. = (4.16)
х—>оо ОХ
Эта задача может быть сведена к уже известному решению задачи об одномерном нестационарном температурном поле при граничных условиях первого рода. Для того чтобы это показать, перейдем к новой переменной — плотности теплового потока
дф(х, т)=-Х^^. (4.17)
ОХ
Продифференцировав уравнение (4.7) по х и, воспользовавшись заменой
(4.17) , преобразуем его к виду
адгФ(х, т) д2дф(х, т) (418)
дт дх2
Краевые условия (4.16) соответственно примут вид
<7Ф(х,0)= 0, q0(O, x)=qc = const, q0(°o, z) = O. (4.19)
Уравнение (4.18) при краевых условиях (4.19) отличается от рассмотренной выше задачи распределения температуры полуограниченного стержня при краевых условиях первого рода только обозначениями. Воспользовавшись известным решением (4.13), запишем
~Яс 2у1озх) Яс у2у1(й х) {2^(ох)
С учетом (4.4) получим [59]
ar(x.’) = _g, erfr х
дх X 2yfm)
|
r(x, x)=^J>rfc |
—dx = л/шт • ierfc —X—, (4.20)
2Vcot ) ^ 2v©x
где ierfcU = ™erfcWdW =-j=e~u2 — UerfcU.
Vit
Значения функций erfcU и ierfcU табулированы и приводятся в специальной литературе [59].
Из (4.20), в частности, следует, что при постоянном тепловом потоке на торце «стержня» его температура прямо пропорциональна плотности теплового потока, обратно пропорциональна коэффициенту аккумуляции тепла и будет повышаться с течением времени пропорционально корню квадратному от времени нагрева
‘ 2 Яс _ 2 Я* ^ _ 2 qc г
где Є = y]xcv.
Процессы распространения тепла в движущиеся стружки и деталь характеризуются весьма малыми значениями времени нагрева (тысячные или даже десятитысячные доли секунды) и большими плотностями тепловых потоков. В связи с этим в зоне резания в течение очень коротких отрезков времени могут возникать очень высокие температуры (порядка 1000 °С).


 2 августа, 2014
2 августа, 2014  Menedjer
Menedjer 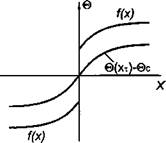
 Опубликовано в рубрике
Опубликовано в рубрике